Pfizer hat den Covid-Impfstoff von Biontec an Babys im Alter zwischen 6 und 23 Monaten getestet. Die Ergebnisse wurden der FDA vorgelegt, im Zuge der entsprechenden Notfallzulassung.
Die Dokumente finden sich hier: https://www.fda.gov/media/159195/download
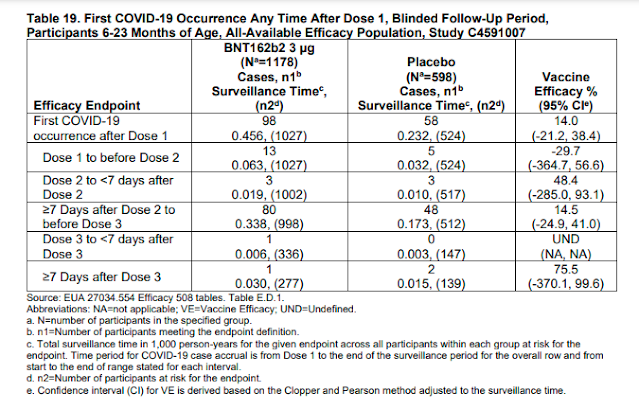
Auf Seite 39 finden sich die folgenden empirischen Angaben zur Wirksamkeit der Impfung. Diese möchte ich hier für Laien verständlich erklären.
Die erste Spalte gibt an, was eigentlich untersucht wurde (Efficacy Endpoint). Es geht um die Anzahl der Covid-Fälle, die nach der Impfung bei der Untersuchten Population eingetreten sind. Die zweite Spalte zeigt die Fälle für die Babys, die den Impfstoff bekommen haben, die dritte Spalte enthält die Placebo-Gruppe (diesen Babys wurde also im gleichen Zeitintervall ein Placebo verabreicht). Die vierte Spalte berechnet basierend auf den Werten von Spalte zwei und drei die Impfwirksamkeit (Vaccine Efficacy).
Schauen wir uns die erste Zeile einmal im Detail an:
Was genau wird hier untersucht? Die erste Spalte enthält ja den Endpoint. Die Falldefinition findet sich ganz am Ende des Dokuments (S. 66). Als Covid-19-Fall gilt also ein positiver NAT-Test (Nukleinsäure-Amplifikations-Technik, also zum Beispiel PCR) mit zusätzlichen Symptomen. Gezählt werde alle Fälle ab dem Tag der ersten Impfung. Dabei wurden sowohl Personen berücksichtigt, die bereits an Covid erkrankt waren als auch solche, die noch keine Covid-Infektion hatten (S. 36). Das ist ein interessantes Detail, auf das ich später noch eingehen werde. Ebenfalls zu berücksichtigen ist, dass nur die erste Infektion gezählt wird. Wenn sich also Personen mehrfach angesteckt haben (und das war der Fall), geht nur das erste mal in die Statistik ein. Auch das ist durchaus erwähnenswert.
In der zweiten Spalte sehen wir jetzt, dass sich 98 von 1027 Personen, die den Impfstoff bekommen haben, mit Covid infiziert haben. Die Zahl 0.456 rechnet das in Personenjahre um und ist für unsere Betrachtung nicht bedeutend. In der dritten Spalte sehen wir, dass sich 58 von 524 Personen, die das Placebo erhalten haben, infiziert haben. Das Verhältnis von Infizierten an der Gesamtgruppe bezeichnet man auch als attack rate. Die Geimpften haben also eine attack rate von 98/1027=0.095. Das heißt, 9.5% der Geimpften haben sich infiziert. Die Ungeimpften haben eine attack rate von 58/524=0.11. Es haben sich also 11% der Ungeimpften infiziert.
Aus diesen attack rates lässt sich nun die Impfwirksamkeit (Vaccine Efficacy, VE) berechnen, die in der vierten Spalte angegeben ist. Die Vaccine Efficacy sagt, wieviel Prozent der Fälle durch die Impfung verhindert werden können. Dafür berechnet man die attack rate der Ungeimpften minus die attack rate der Geimpften (also um wie viel wurde die attack rate durch die Impfung gesenkt) und teilt dies durch die attack rate der ungeimpften (also was wäre die Gesamtheit, wenn niemand geimpft wäre). Für die klassische Prozentdarstellung wird dieser Wert dann noch mit 100 multipliziert.
Also gerundet (0.11-0.095)/0.11=0.14*100, was den 14 Prozent entspricht, die in der vierten Spalte angegeben sind. (Zumindest sollte es den Werten entsprechen. Merkwürdiger Weise weichen die Pfizer zahlen alle leicht nach oben ab. Der exakte Wert wäre 0.138, also 13.8% nicht 14.0%.)
Ansonsten gibt es noch Angaben zum Konfidenzintervall (die Werte -21.2 und 38.4). Diese Werte sagen uns, dass man mit einer 95% Wahrscheinlichkeit davon ausgehen kann, dass der tatsächliche Wert der Impfwirksamkeit irgendwo zwischen -21.2% und 38.4% liegt. Statistisch gesprochen ist das nicht ganz korrekt: Die Konfidenzintervalle sind abhängig vom Verfahren – hier das Clopper Pearson Verfahren. Wenn man genau ist, müsste man also sagen, dass es eine 95%-Wahrscheinlichkeit gibt, dass bei Nutzung des Clopper Pearson Verfahrens der tatsächliche Wert der Impfwirksamkeit in dem Intervall liegt. Wer die Konfidenzintervalle reproduzieren möchte, findet übrigens hier ein Tutorial: https://digitalcommons.usf.edu/cgi/viewcontent.cgi?article=1390&context=numeracy
Die folgenden Zeilen schlüsseln nun die 98 bzw. 58 Fälle nach der Zeit auf, wann sie eingetreten sind. Dabei ist zu beachten, dass die Zeitabschnitte unterschiedlich lang sind, zum Beispiel eine Woche nach der zweiten Impfung, aber dann bis zur dritten Impfung. Daher sind die absoluten Zahlen in den Zeilen unterschiedlich. Das Verhältnis der Fälle bei den Geimpften zu den Fällen der Ungeimpften kann aber in der Impfwirksamkeit berechnet werden.
Achtet man nur auf die VE, dann könnte der Eindruck entstehen, die erste Dosis hilft wenig (schadet vielleicht sogar, weil negative Impfwirksamkeit) aber spätestens die dritte Dosis bringt es dann voll mit einer Impfwirksamkeit von 75.5%. Diese Interpretation ist aber statistisch nicht zulässig. Wir müssen die Konfidenzintervalle beachten. Den in Wirklichkeit sagt die letzte Zeile zum Beispiel, dass die tatsächliche Wirksamkeit nach der dritten Impfung (bei gegebenem CI-Verfahren) mit 95%-Wahrscheinlichkeit irgendwo zwischen -370.1% und 99.6% liegt. Mit anderen Worten: Es kann nicht ausgeschlossen werden, dass sich Dreifachgeimpfte in der Woche nach der letzten Spritze 3,7-mal so oft infizieren wie Ungeimpfte. Die Konfidenzintervalle werden in der Zeitabschnitten so riesig, weil die Gesamtzahl der Fälle so gering ist. Selbst aber auf die komplette Zeit bezogen ist die Studie nicht signifikant. Auch in Zeile eins geht das Konfidenzintervall vom Minusbereich (-21.2) bis in den positiven Bereich. Mit der Signifikanz muss man sich das so vorstellen: Würde man die Studie hundert Mal mit unterschiedlichen Probanden wiederholen, dann würden wir davon ausgehen, dass die Wirksamkeit nur in fünf Fällen höher als 38.4% oder niedriger als -21.2% wäre. Das heißt aber eben auch, dass bei den 95 Studien welche dabei wären, wo die Wirksamkeit zwischen -21.2% und 0% liegt. Wir können daher nicht mit ausreichender Sicherheit davon ausgehen, dass die Impfung überhaupt einen positiven Effekt hat. Sie könnte auch negativ wirken, so dass häufiger Erkrankungen auftreten als ohne Impfung.
Und selbst die errechnete Impfwirksamkeit von 14% ist ziemlich wenig (zumal wir inzwischen ja davon ausgehen, dass die Wirksamkeit schnell nachlässt). Gehen wir mal als Beispiel davon aus, dass es 1,6 Millionen Kinder in Deutschland zwischen 6 Monaten und zwei Jahren gibt (die Zahl ist eine Schätzung basierend auf der Geburtenanzahl von rund 800.000). Gehen wir weiter davon aus, dass jede dieser Personen sich mit dem Covid-Virus infiziert. Gehen wir außerdem davon aus, dass die Wirksamkeit der Impfung tatsächlich 14% ist (was statistisch unzulässig ist, siehe oben). Dann würden ohne Impfung 11% der Kinder erkranken, also 176.000. Würden alle Kinder geimpft, dann wären es immer noch 152.000. Für diese Reduzierung müsste man aber eben alle 1,6 Millionen Kinder impfen und das, obwohl es in der gesamten Studie nur einen einzigen Fall eines schweren Krankheitsverlaufs gab (S. 37).
---
Abschließend sei noch auf zwei „blinde Flecken“ in der Studie hingewiesen: Wie oben erwähnt werden auch die Fälle mitgezählt, in denen es bereits Covid-Erkrankungen gab, also Kinder schon genesen sind. Ohne zu wissen, wie sich diese Gruppe auf Geimpfte und Ungeimpfte verteilt, lässt sich keine Aussage über die Impfwirksamkeit machen. Es könnte ja sein, das überproportional viele Genesene im Impfarm oder im Placeboarm waren und wir gar nicht die Wirkung der Impfung sondern der Genesung sehen bzw. die Impfung eigentlich viel besser wirkt. Ebenfalls merkwürdig ist, dass mehrfach Infektionen nicht gezählt werden. Auch hier ist es möglich, dass der Effekt ungleich über die Gruppen verteilt sind. Vielleicht infizieren sich Ungeimpfte oder Geimpfte öfter. Das würde die Risikokalkulation sehr beeinflussen.