Die Einschätzung, wie effektiv die COVID-Impfung ist, ist eine der politisch relevantesten Kennzahlen derzeit. Insbesondere für die Einschätzungen der Angemessenheit einr Impfpflicht ist diese Zahl extrem wichtig. In der Vergangenheit hat sich immer wieder gezeigt, dass die Berechnungen des RKI nicht in jeder Hinsicht eindeutig sind, sondern auf vielen Annahmen beruhen, die man auch kritisch hinterfragen kann und muss. Für die politische Datenwissenschaft ist es daher essenziell, diese Berechnungen nachvollziehbar zu machen.
In diesem Beitrag wird das methodische Vorgehen des RKI zur Berechnung der Impfeffektivität analysiert. Die Informationen dazu entstammen den RKI-Wochenberichten.
In einem zweiten Teil habe ich die konkreten Berechnungen des RKI so weit wie möglich rekonstruiert und kann daher zeigen, wie stark die Ergebnisse schwanken, wenn Annahmen leicht verändert werden.
Meine Erkenntnisse aus der folgenden Analyse:
Das RKI verwendet zur Berechnung der Impfeffektivität die Methode nach Farrington, die im gegebenen Kontext als fragwürdige erscheinen muss.
Die Berechnungen lassen sich nicht wirklich nachvollziehen, weil die Daten, die in die Berechnung einfließen, nicht zur Verfügung gestellt werden. Es fehlt also an echter Transparenz.
Die Berechnungen lassen zwei entscheidende Größen außer Acht:
1. Die Fälle, für die der Impfstatus nicht bekannt ist, werden einfach ignoriert.
2. Es kann nicht unterschieden werden, welcher Effekt auf die Impfung zurückzuführen ist und welcher auf die Genesung nach Infektion.
Die Ergebnisse sind sehr stark durch bestimmte Annahmen getrieben. Beispielsweise werden die Fälle der letzten vier Wochen auf die Impfquote der letzten vier Wochen bezogen. Dabei ist davon auszugehen, dass insbesondere bei “Tod”, die Infektion länger zurück liegt.
Mein Fazit ist daher, dass die Impfeffektivität, wie sie vom RKI ermittelt wird, nicht die Grundlage für politische Entscheidungen sein sollte.
Wie berechnet das RKI die Impfeffektivität
Zunächst ist festzuhalten, dass die eigentliche Impfeffektivität – nämlich inwiefern die Impfung vor einer Ansteckung mit SARS-CoV-2 schützt – überhaupt nicht erhoben wird. Dabei war dies der Endpunkt der Zulassungsstudien. Die Pfizer-Studie hat z. B. als Ergebnis: “A two-dose regimen of BNT162b2 conferred 95% protection against Covid-19 in persons 16 years of age or older.” (Polack et al. 2020) Dabei ist bereits anzumerken, dass auch Pfizer mit dem Begriff der Infektion unterschiedlich umgeht. In der Studie selbst ging es um symptomatische COVID-Erkrankung. In der Außendarstellung wurde zunächst von Ansteckung allgemein gesprochen und in Deutschland gilt offiziell als „infiziert“ wer einen positives PCR-Testergebnis hat.
Egal, ob die versprochene Effektivität nun wegen der Delta-Variante nicht erreicht wird oder vielleicht außerhalb der Studie nie erreicht wurde: Es gibt Konsens darüber, dass diese Werte so nicht zutreffen. Ob die Impfung überhaupt (noch) gegen Ansteckung hilft und wenn ja wie stark, ist fraglich. Um so wichtiger wäre es, diesen Wert zu ermitteln. Das ist aber mit den vorliegenden Daten nicht möglich, da bei den Tests (positiver PCR-Test gilt per Definition als COVID-Fall) der Impfstatus gar nicht erhoben wird. Stattdessen ermittelt das RKI die Impfeffektivität hinsichtlich der Endpunkte “symptomatische Infektion”, “Hospitalisierung”, “Intensivstation” und “Tod” für verschiedene Altersgruppen. Dabei kommt die Screening-Methode nach Farrington zum Einsatz. Bei dieser Methode wird der Anteil der Geimpften an den Erkrankten in ein Verhältnis gesetzt zum Anteil der Geimpften an der untersuchten Grundgesamtheit nach der folgenden Formel:
mit
VE = Impfeffektivität
PCV = Anteil der Geimpften an den Erkrankten
PPV = Anteil der Geimpften an der Grundgesamtheit
Durch die verschiedenen Gegenwahrscheinlichkeiten (1 – x) ist es sehr schwer abzuschätzen, wie sich diese Formel verhält. Einen ersten Überblick bekommt man dadurch, dass man sich fragt, wann diese Gleichung größer Null ist.
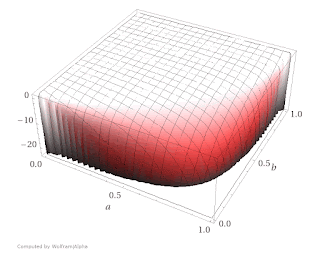
Die Grafik zeigt, die Impfeffektivität wird positiv sein, wenn der Anteil der Geimpften an der Grundgesamtheit größer ist, als der Anteil der Geimpften an den Erkrankten (da es sich um prozentuale Anteile handelt, können PCV und PPV nur Werte zwischen 0 und 1 einnehmen). Das erscheint unmittelbar logisch. Aber wie verhalten sich die Werte der Impfeffektivität bei unterschiedlichen Quoten? Die nächste Abbildung zeigt den Wertebereich:
Die Grafik zeigt, dass bei einer hohen Impfquote (im Plot b) der Anteil der Geimpften an den Erkrankten (a) schon sehr hoch sein muss, um aus dem völligen Sättingungsbereich zu kommen. Die Werte auf der y-Achse zeigen die mögliche Impfeffektivität. In den Randbereichen werden diese Werte stark negativ. Das wäre der Fall, wenn zum Beispiel mehr Geimpfte als Ungeimpfte erkranken. Sobald aber entweder der Anteil der Geimpften an den Erkrankten sehr niedrig ist ODER die Impfquote sehr hoch ist, kann die Funktion nur Werte produzieren, die nahe 1 sind (also für eine sehr hohe Impfeffektivität sprechen. In anderen Worten: Die Methode wird bei einer hohen Impfquote fast immer eine hohe Effektivität ermitteln. Diese Probleme mit der Farrington-Methode wurden von Cohen et al. 2012 aufgezeigt. Die Autoren kommen zu dem sehr eindeutigen Ergebnis: “In summary, the screening method should only be used as a preliminary test in situations where the data inputs are valid, more reliable evaluations of vaccine impact are not feasible, where sufficient cases are available, and vaccine coverage has not peaked in the general population.”
Schon vor diesem Hintergrund stellt sich somit die Frage, ob sich eine evidenzbasierte Politik an einen solchen Wert halten sollte, wenn es immer wieder massive Zweifel an der Datenqualität gibt, die Zahl der Fälle für die Endpunkte Intensivstation und Tod (zumal bei den jüngeren Altersgruppen) sehr gering ist und die Mehrheit der Bevölkerung geimpft ist. Mein Schluss wäre bereits hier, dass die Methode fragwürdig ist und die Ergebnisse mit äußerster Vorsicht betrachtet werden müssen und keine verlässliche Grundlage für politische Entscheidungen abgeben.
Details, die Fragen aufwerfen
Im RKI-Wochenbericht finden sich dann einige Details zur Berechnung der Impfeffektivität, die die Skepsis verstärken. Zunächst einmal gibt es zwei verschiedene Berechnungen: Einmal wird die Impfeffektivität auf die gesammelten Impfdurchbrüche der letzten vier Wochen bezogen. In der Abbildung 19 im Wochenbericht wird hingegen eine wöchentliche Darstellung präsentiert. Wöchentliche Zahlen zu den Impfdurchbrüchen liegen aber nicht vor, sondern nur die aggregierten Zahlen der letzten Wochen.
Starke Schwankungen = Schlechte Datenlage
Bei der wöchentlichen Darstellung fällt auf, dass sich beim Endpunkt “Symptomatische Erkrankung” die Impfeffektivität zwischen den Altersgruppen stark unterscheidet. Für die 12-17 Jährigen wird eine wesentliche höhere Effektivität ermittelt. Die Zulassungsstudie von Biontec ging aber davon aus, dass es keine signifikanten Unterschiede zwischen Altersgruppen gibt. (“Supplemental analyses indicated that vaccine efficacy among subgroups defined by age, sex, race, ethnicity, obesity, and presence of a coexisting condition was generally consistent with that observed in the overall population”, Polack et al. 2020).
Entweder, wir sehen hier also einen Effekt, der in der klinischen Studie nicht erkennbar war, oder es gibt eine Verzerrung in den Daten.
Ebenfalls auffällig ist, dass die Effektivität (beim Endpunkt „Symptomatisch“) bei den über 60-Jährigen in den letzten Wochen rapide gestiegen ist, von 63% auf 80%. Dass die Effektivität der Impfung nachlässt, gilt inzwischen als Common Sense und begründet derzeit vor allem die Notwendigkeit der Booster Impfungen. Wie aber ist zu erklären, dass die Impfung plötzlich 17% an Effektivität gewinnt? Dies ist ein klares Signal für eine unzuverlässige Datenbasis und zwar nicht nur – wie auch das RKI einräumt – in Bezug auf die letzten Wochen sondern auf die komplette Zeitreihe. Bei den Endpunkten “Hospitalisierung” und “Tod” sehen wir Sprünge von 30% und 20%. Offenbar sind die Fallzahlen nicht ausreichend, um eine solide Schätzung vorzunehmen. Das ist auch der Grund, warum die Impfeffektivität für 12-17-Jährige nicht in Bezug auf die Endpunkte “Intensivstation” und “Tod” angegeben werden. (RKI-Wochenbericht: “Für die Altersgruppe der 12- bis 17-Jährigen erfolgte aufgrund der geringen Fallzahlen von Behandlungen auf einer Intensivstation bzw. von Todesfällen in der Gruppe der Ungeimpften und fehlenden Fällen in der Gruppe der Geimpften nur die Berechnung der Impfeffektivität gegenüber einer symptomatischen Erkrankung bzw. Hospitalisierung.”) Hier ist anzumerken: Das RKI hat offenkundig einen internen Maßstab, ab wann die Fallzahl als zu gering eingeschätzt wird, um die Effektivität zu berechnen. Dieser Maßstab ist aber nicht bekannt.
[Ungeimpft + Geimpft] + ? Welche Fälle gehen (nicht) in die Berechnung ein?
Die mangelhafte Datengrundlage wird auch der Grund sein, warum das RKI die Daten für vier Wochen aggregiert. Allerdings wirft die Berechnungsweise ebenfalls Fragen auf: Das RKI bezieht sich nur auf die Fälle, bei denen der Impfstatus bekannter Maßen geimpft oder ungeimpft ist und zwar sowohl bei den Impfdurchbrüchen (also PCV in der Farrington-Formel) als auch bei der Impfquote (PPV). Das klingt erst mal gut – gerade angesichts der Meldungen, dass in Bayern und Hamburg die Fälle, bei denen der Status als unbekannt galt einfach als ungeimpft gezählt wurden. Das RKI agiert hier also wesentlich sauberer als die Gesundheitsämter in Hamburg und Bayern. Methodisch wirft aber auch das „Rausrechnen“ der unbekannten Fälle einige Fragen auf und hat Konsequenzen für die Berechnung. Zunächst einmal muss man sich klar machen, dass der Impfstatus nicht binär ist. Neben den Geimpften und den Ungeimpften gibt es mindestens zwei weitere Gruppen: Unbekannt und unvollständig geimpft. Das Wegnehmen dieser beiden Gruppen verändert die Grundgesamtheit und dies kann sich bei einer Formel wie der Farrington-Methode schnell sehr stark auswirken. Bei den unbekannten Fällen kommt es darauf an, wie sich Geimpfte und Ungeimpfte (und unvollständig Geimpfte) auf diese Gruppe verteilen. Da die Fallzahlen für einige Endpunkte offenbar kaum reichen, könnten die Unbekannten die Impfeffektivität vermutlich in beide Richtungen stark beeinflussen. Sind mehr Unbekannte Ungeimpft (in Relation zum bereits bekannten Verhältnis der Impfdurchbrüche), dann wäre die Effektivität eventuell deutlich höher. Sind es mehr Geimpfte, dann könnte die Effektivität drastisch sinken.
Auch das Herausnehmen der unvollständig Geimpften ist nicht trivial. Die Gruppe der unvollständig Geimpften kann weder den Ungeimpften noch den Geimpften zugeschlagen werden. Das Vorgehen des RKI ist hier also erst einmal positiv zu werten. Aber: Dadurch verändert sich die Grundgesamtheit, wie sie in der Farrington-Methode erscheint, erneut. Als Statistiker würde man sich fragen, ob die Gruppe der Ungeimpften zusammen mit den vollständig Geimpften ein repräsentatives Sample der Gesamtbevölkerung ist. Ein weiterreichender Ansatz könnte einfach die Impfeffektivität für diese Gruppe ebenfalls angeben. Generell wäre ja die Annahme, dass die Impfung auch schon eine Wirkung hat, bevor die 14 Tage nach der zweiten Impfung abgelaufen sind. Es wäre also sinnvoll, die Effektivität auch für die unvollständig Geimpften zu ermitteln. Würde sich zeigen, dass die Impfung auch schon nach der ersten Dosis eine hohe Effektivität hat, spräche dies ja für die Impfung. Theoretisch wäre es allerdings auch denkbar, dass die Effektivität nach nur einer Impfung negativ ist, dass also mehr Infektionen entstehen. In einem solchen Fall würde das die Einschätzung der Impfung negativ tangieren. Die Daten liegen vor, das RKI könnte dazu Auskunft geben.
Ist die Impfquote zu hoch oder zu niedrig?
Aus der Entscheidung, nur die explizit geimpften und ungeimpften Fälle zu betrachten, folgt eine schwerwiegende Veränderung der PPV-Variable in der Farrington-Formel. Der Anteil der Geimpften an der Grundgesamtheit ist jetzt nicht mehr identisch mit der Impfquote! Statt dessen wird das Verhältnis von Geimpften zu der Gruppe der Geimpften und Ungeimpften genommen. Auch dies ist eine Design-Entscheidung und nicht verkehrt, aber eben folgenreich. Denn: Das Verhältnis der Geimpften zu Ungeimpft + Geimpft muss notwendig höher sein, als die Impfquote, die die Geimpften in der Altersgruppe zur Bevölkerung ins Verhältnis setzt. Schon aus der theoretischen Betrachtung der Farrington-Formel sowie aus der Analyse von Cohen et al. 2012 wissen wir, dass die Schätzung der Impfeffektivität sehr sensibel auf hohe PPV-Werte reagiert, so dass prinzipiell eine hohe Effektivität geschätzt wird. Die berechnete Impfeffektivität kann daher nicht als eine allgemeine Aussage über die Impfung verstanden werden. Genaugenommen müsste es heißen, das RKI berechnet die Impfeffektivität für die Gruppe der bekannten (!) Fälle, die geimpft oder ungeimpft sind. Die tatsächliche Impfeffektivität in der Bevölkerung kann von diesen Werten abweichen.
Vielleicht ist die Impfquote aber auch viel zu niedrig. Das RKI geht selbst von einer Untererfassung von bis zu 5% aus. Dass müsste sich dann auch auf die Effektivität der Impfung auswirken.
Auf welche Zeit bezieht sich die Impfquote?
Das RKI verwendet für die Berechnung der “Impfquote” (eigentlich Verhältnis Geimpft zu Geimpft + Ungeimpft, PPV in der Farrington-Formel) den Durchschnitt der letzten vier Wochen. Auch das klingt zunächst vernünftig. Aber: Die Impfquote erreicht eine Sättigung. D. h. in der Regel werden jede Woche weniger Impfungen hinzu kommen, aber die Zahl der Impfungen wird weiter steigen. Durch diesen Wachstumsprozess wird der errechnete Mittelwert stärker von den niedrigeren Werten (vor vier Wochen) abweichen, als von den aktuelleren Werten. Eigentlich verwendet man daher in der Statistik für Wachstumsprozesse nicht das arithmetische Mittel, sondern das geometrische Mittel (alle Werte werden multipliziert, dann wird die n-te Wurzel gebildet). Das geometrische Mittel hat den Vorteil, dass bei zwei Werten das Minimum und das Maximum um den gleichen Faktor abweichen. Bei den Zahlen 1 und 9 wäre das arithmetische Mittel 4.5, das geometrische 3. Sowohl der niedrige Wert 1 wie auch der hohe Wert 9 sind vom Mittelwert 3 um Faktor 3 entfernt. Wird aber das arithmetische Mittel genommen, dann wird die Impfquote systematisch überschätzt. Erstens ist das arithmetische Mittel immer größer/gleich dem geometrischen. Zweitens bekommen dadurch die letzten Wochen mit bereits höherer Impfquote ein stärkeres Gewicht. Wie sich – selbst kleine Differenzen – letzten Endes auf die Impfeffektivität auswirken, ist zu überprüfen.
Eine weitere offene Frage ist, ob überhaupt mit den richtigen Zeiträumen gearbeitet wird. Denn das RKI vergleicht die Fälle, bei denen momentan Symptome, eine Hospitalisierung, eine Behandlung auf der Intensiv oder Tod gemeldet (!) werden, mit den aktuellen Impfquoten. Wenn jemand heute stirbt (bzw. heute der Tod gemeldet wird) dann ist davon auszugehen, dass die Infektion schon länger zurück liegt. Eigentlich wäre es logisch, die Impfquoten zum Zeitpunkt der Infektion zu berechnen. Und auch hier ist klar, dass der Weg des RKI die Impfquoten systematisch überschätzt, da die Zahl der Impfungen ja konstant zunimmt. Würde man diese Zeitverzögerung einkalkulieren, dann müsste man eigentlich die Impfquote zum Zeitpunkt der Ansteckung ermitteln. Die läge dann aber naturgemäß unter der Impfquote, die das RKI verwendet.
Wo sind die Genesenen?
Eine wichtige Frage bei kritischen Datenstudien ist auch immer, was eigentlich nicht erfasst wird. Alle Berechnungen des RKI weisen einen auffälligen blinden Fleck auf. Nach 20 Monaten Pandemie sind bereits sehr viele Menschen mit COVID in Kontakt gekommen und sind genesen. Nach offizieller Lesart sind das alle, die einen positiven PCR-Test hatten und nicht verstorben sind, also ca. 6,5 Millionen. Hinzu kommt noch eine unbekannte Dunkelziffer von Leuten, die genesen sind, ohne dass sie vorher einen Test gemacht haben (zum Beispiel bei milden Symptomen). Es herrscht erstens Einigkeit darüber, dass ein überstandener Kontakt mit dem Virus in der Regel zu einer positiven Immunantwort führt und diese Personen einen Schutz vor weiteren Infektionen haben. Es ist zweitens gesichert – und geht auch aus den Berichten des RKI hervor –, dass Geimpfte sich ebenfalls infizieren. Drittens sagt zum Beispiel Christian Drosten, dass Geimpfte, die sich zusätzlich infizieren und genesen, einen höheren Schutz haben, als nur durch die Impfung. Insofern gibt es zwangsläufig Genesene in der Gruppe der Geimpften und der Ungeimpften. Ohne diese Gruppe zu identifizieren, lassen sich keine wirklichen Aussagen über die Effektivität der Impfung machen. Denn wenn überproportional Genesene bei den Ungeimpften sind, dann wäre die Impfung wesentlich effektiver als sie erscheint. Man würde dann den Effekt der Impfung im Vergleich zu einer teilweise erlangten natürlichen Immunisierung messen, nicht aber die Wirksamkeit der Impfung. Umgekehrt: Wenn unter den Geimpften mehr Genesene sind, dann ist das, was wie der Effekt der Impfung aussieht in Wirklichkeit zum Teil ein Effekt der natürlichen Immunisierung. Damit ist auch klar, dass absolute Zahlen (wie die Inzidenz) nicht interpretiert werden können, ohne dass man weiß, wer bereits genesen ist. Unabhängig davon, wie sich die Genesenen auf die Gruppen verteilen, ist es absolut unbestreitbar, dass mit dem methodischen Vorgehen des RKI der Effekt der Impfung mit dem Effekt der fortschreitenden Immunisierung in der Bevölkerung vermischt wird!
Fazit zum theoretischen Teil: Die Impfeffektivität ist keine verlässliche Zahl
Es ist gezeigt worden, dass die Datenlage mangelhaft ist sowohl hinsichtlich der Qualität als auch der Quantität, dass die Impfquote unsicher ist und von der Methode der Berechnung systematisch überschätzt wird und dass wichtige Größen völlig unbekannt sind und nicht in die Berechnung eingehen. Die Berechnungen sind nicht falsch, aber sie enthalten so viele Unsicherheiten, dass man diese Kennzahlen nicht als verlässliche Basis für weitreichende politische Entscheidungen ansehen kann. Die Warnung von Cohen et al., man solle diese Methode nur benutzen, wenn andere Erhebungsmöglichkeiten nicht gegeben sind, ist absolut relevant, zumal wir hier mit schlechten Daten, geringen Fallzahlen und hoher Impfquote genau den Fall vor uns haben, von dem die Autoren sagen, dass die Farrington-Methode systematisch versagt.
Immer wieder wütet in den politischen Debatten ein Funktionalismus im Umgang mit Daten, der jede Kritik an der Datengrundlage mit dem Verweis kontert, andere Daten wären nun einmal nicht vorhanden. Diese Einstellung, die zu einer immensen Zahl an falschen Analysen (meist unter dem Stichwort “datamining”) geführt hat, ist wissenschaftlich nicht zu tolerieren. Entweder, die Daten sind verlässlich, oder die Erkenntnisse, die daraus abgeleitet werden, sind es auch nicht. Die hier beschriebenen Unwägbarkeiten sind eben nicht rein theoretisch, sondern wirken sich notwendig auf die Analyse aus. Wissenschaftlich wäre es, das eigene Unwissen zu akzeptieren und transparent zu kommunizieren, nicht aber, auf Basis falscher Daten Entscheidungen zu treffen. Nach 20 Monaten Pandemie ist es sowieso ein politischer Skandal, dass die Datenlage so ist, wie sie ist.
Im Fall der Impfeffektivität ist es sogar noch schlimmer. Denn hier verfügt das RKI über Daten, die aber nur stückchenweise bereitgestellt werden. Man kann daher nur vermuten, welchen Einfluss die genannten Punkte haben könnten.
Um einen Schritt weiter zu kommen, versuche ich im nächsten Teil dieses Beitrags die Daten so weit wie möglich “nachzubauen”. Dafür rechne ich aus der gemeldeten Inzidenz die Fallzahlen zurück und rekonstruiere die Impfeffektivität. Dieser Ansatz hat zwei Vorteile. Erstens wird deutlich, wie genau das RKI rechnet und welche Teufel in den Details stecken können. Zweitens entsteht dadurch die Möglichkeit, selbst Szenarien zu berechnen. Was wäre, wenn die Unbekannten Fälle überwiegend geimpft/ungeimpft sind? Wie verändert sich die Impfquote, wenn man ein Timelag einberechnet? Wie hoch wäre die Impfeffektivität, wenn die Impfquote um 5% höher ist? Solche Fragen lassen sich beantworten, wenn es gelingt, die Berechnung des RKI zu rekonstruieren.